Prisma (geometri)
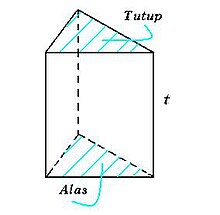
Dalam geometri, prisma adalah bangun ruang tiga dimensi yang dibatasi oleh alas dan tutup identik berbentuk segi-n dan sisi-sisi tegak berbentuk segiempat. Dengan kata lain prisma adalah bangun ruang yang mempunyai penampang melintang yang selalu sama dalam bentuk dan ukuran.
Limas dengan alas dan tutup berbentuk persegi disebut balok sedangkan prisma dengan alas dan tutup berbentuk lingkaran disebut tabung.
Rumus Prisma
Luas permukaan
Luas permukaan prisma dengan alas dan tutup segi-n dapat dihitung dengan rumus berikut:

Volume

Tabung (geometri)
Dalam geometri, tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Kubus memiliki 3 sisi dan 2 rusuk.
Kedua lingkaran disebut sebagai alas dan tutup tabung serta persegi panjang yang menyelimutinya disebut sebagai selimut tabung.
Rumus tabung
Luas alas
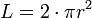
Luas selimut

Luas permukaan
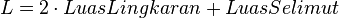

Volume

Limas (geometri)
Dalam geometri, limas adalah bangun ruang tiga dimensi yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga.
Kerucut dapat disebut sebagai limas dengan alas berbentuk lingkaran.
Limas dengan alas berupa persegi disebut juga piramida.
Rumus limas
Luas permukaan
Luas permukaan limas dengan alas segi-n dapat dihitung dengan rumus berikut:

Volume

Kubus
Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang berbentuk bujur sangkar. Kubus memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Kubus juga disebut bidang enam beraturan, selain itu juga merupakan bentuk khusus dalam prisma segiempat.
Rumus
Bila variabel s adalah panjang sisi kubus
Rumus kubus
Luas
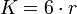
Volume
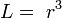
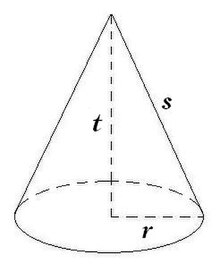
Kerucut
Dalam geometri, kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk.
Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang lengkung yang disebut selimut kerucut.
Rumus kerucut
Luas alas
L = πr2
Luas selimut

Luas permukaan
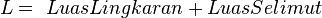

Volume
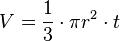
Bola (geometri)
Dalam geometri, bola adalah bangun ruang tiga dimensi yang dibentuk oleh tak hingga lingkaran berjari-jari sama panjang dan berpusat pada satu titik yang sama. Bola hanya memiliki 1 sisi.
Rumus bola
Luas permukaan
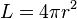
Volume
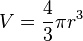
Balok
Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang, dengan paling tidak satu pasang diantaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok yang dibentuk oleh enam persegi sama dan sebangun disebut sebagai kubus.
Elemen balok
- Panjang (p) adalah rusuk terpanjang dari alas balok.
- Lebar (l) adalah rusuk terpendek dari sisi alas balok.
- Tinggi (t) adalah rusuk yang tegak lurus terhadap panjang dan lebar balok.
Rumus balok
Luas permukaan

Volume

Panjang diagonal ruang
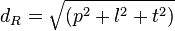
Panjang diagonal bidang


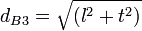
Luas bidang diagonal









Assalamualaikum, saya tertarik dengan artikel anda. Tapi ada yang mengganjal, yakni ada yang mengatakan bahwa bagian puncak dari kerucut bukan titik sudut, karena kalau beranggapan pada konsep titik sudut maka berarti bertitik sudut tak hingga pada kerucut. Maka daripada itu, jika kerucut tak memiliki titik sudut, maka kerucut tidak dapat dikatakan limas. Mohon penjelasannya.Terima kasih
BalasHapusbodoh gk pinter ngblogger
BalasHapus